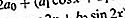Euklidovská geometria
Ak vezmeme do úvahy euklidovskú geometriu, zreteľne zistíme, že odkazuje na zákony upravujúce polohu tuhých telies. Obracia sa na účet geniálnej myšlienky spätného sledovania všetkých vzťahov týkajúcich sa tiel a ich relatívnych pozícií až po veľmi jednoduchý koncept „vzdialenosť“ (Strecke). Vzdialenosť označuje pevné teleso, na ktorom boli špecifikované dva materiálové body (značky). Pojem rovnosti vzdialeností (a uhlov) sa vzťahuje na experimenty zahŕňajúce náhody; rovnaké poznámky platia pre vety o zhode. Euklidovská geometria teraz v podobe, v akej nám bola odovzdaná od Euklidu, používa základné pojmy „priamka“ a „rovina“, ktoré, ako sa zdá, nezodpovedajú alebo v žiadnom prípade nie priamo súvisia so skúsenosťami o postavení tuhých telies. K tomu je potrebné poznamenať, že pojem priamky sa môže zredukovať na koncept vzdialenosti.1 Okrem toho sa geometrici menej zaujímali o to, ako vyjadriť vzťah svojich základných pojmov k zážitkom, ako logicky odvodiť geometrické výroky z niekoľkých axiómov, ktoré boli na začiatku odhalené.
Stručne načrtneme, ako možno z euklidovskej geometrie možno získať koncept pojmu vzdialenosť.
Začneme od rovnosti vzdialeností (axióma rovnosti vzdialeností). Predpokladajme, že z dvoch nerovnakých vzdialeností je jedna vždy väčšia ako druhá. Rovnaké axiómy platia pre nerovnosť vzdialeností ako pre nerovnosť čísel.
Tri vzdialenosti AB 1, BC 1, CA 1 môžu, ak je vhodne zvolené CA 1, mať svoje značky BB 1, CC 1, AA 1 na sebe umiestnené takým spôsobom, že vznikne trojuholník ABC. Vzdialenosť CA 1 má hornú hranicu, pre ktorú je táto konštrukcia stále možná. Body A, (BB ') a C potom ležia v „priamke“ (definícia). To vedie k koncepciám: vytvorenie vzdialenosti o sumu rovnajúcu sa jej; rozdelenie vzdialenosti na rovnaké časti; vyjadrenie vzdialenosti pomocou čísla pomocou meracej tyčinky (definícia intervalu medzi dvoma bodmi).
Ak sa takto získa koncept intervalu medzi dvoma bodmi alebo dĺžka vzdialenosti, potrebujeme iba nasledujúci axiom (Pythagorov teorém), aby sme analyticky dospeli k euklidovskej geometrii.
Ku každému bodu v priestore (referenčné číslo) môžu byť priradené tri čísla (súradnice) x, y, z - a naopak - takým spôsobom, že pre každú dvojicu bodov A (x 1, y 1, z 1) a B (x 2, y 2, z 2) veta platí:
číslo opatrenia AB = odmocniny {(x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2 }.
Všetky ďalšie koncepty a návrhy euklidovskej geometrie môžu byť na tomto základe vytvorené logicky, najmä tiež návrhy týkajúce sa priamky a roviny.
Zámerom týchto poznámok samozrejme nie je nahradiť striktne axiomatickú konštrukciu euklidovskej geometrie. Chceme iba hodnoverne naznačiť, ako možno všetky koncepcie geometrie vysledovať až po koncepciu vzdialenosti. Rovnako tak by sme mohli v poslednom vyššie uvedenom vety predstavovať celú euklidovskú geometriu. Vzťah k základom skúseností by sa potom poskytol prostredníctvom doplnkovej vety.
Súradnica sa môže a musí byť vybraná tak, aby sa dva páry bodov oddelené rovnakými intervalmi, vypočítané pomocou Pythagorovej vety, mohli zhodovať s jednou a tou istou vhodne zvolenou vzdialenosťou (na pevnej látke).
Koncepcie a návrhy euklidovskej geometrie sa môžu odvodiť z tvrdenia Pytagora bez zavedenia tuhých telies; ale tieto koncepcie a návrhy by potom nemali obsah, ktorý by bolo možné otestovať. Nejde o „pravdivé“ výroky, ale iba o logicky správne výroky čisto formálneho obsahu.