Vektorová analýza, odvetvie matematiky, ktoré sa zaoberá množstvami, ktoré majú tak veľkosť, ako aj smer. Niektoré fyzikálne a geometrické veličiny, nazývané skaláre, sa dajú úplne definovať špecifikovaním ich veľkosti vo vhodných merných jednotkách. Teda hmotnosť môže byť vyjadrená v gramoch, teplota v stupňoch v určitom meradle a čas v sekundách. Skaláre môžu byť graficky znázornené bodmi v určitej číselnej mierke, ako sú hodiny alebo teplomer. Existujú tiež veličiny, nazývané vektory, ktoré vyžadujú špecifikáciu smeru a veľkosti. Rýchlosť, sila a posun sú príklady vektorov. Množstvo vektora môže byť graficky znázornené segmentom riadenej čiary, ktorý je symbolom šípky smerujúcej v smere množstva vektora, pričom dĺžka segmentu predstavuje veľkosť vektora.
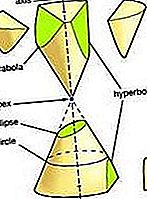
analytická geometria: Vektorová analýza
V euklidovskom priestore ľubovoľnej dimenzie môžu byť vektory - smerované úsečky - určené súradnicami. N-tica (a1, ,
Vektorová algebra.
Prototypom vektora je riadený úsečka AB (pozri obrázok 1), o ktorej sa dá predpokladať, že predstavuje posun častice z jej počiatočnej polohy A do novej polohy B. Na rozlíšenie vektorov od skalárov je obvyklé označovať vektory pomocou tučným písmom. Vektor AB na obrázku 1 môže byť označený a a jeho dĺžka (alebo veľkosť) pomocou | a |. V mnohých problémoch je umiestnenie počiatočného bodu vektora nepodstatné, takže dva vektory sa považujú za rovnaké, ak majú rovnakú dĺžku a rovnaký smer.

Rovnosť dvoch vektorov aab je označená obvyklým symbolickým zápisom a = b a užitočné definície elementárnych algebraických operácií na vektoroch sú navrhnuté pomocou geometrie. Ak teda AB = a na obrázku 1 predstavuje posun častice z A do B a následne sa častica presunie do polohy C, takže BC = b, je zrejmé, že posun z A do C možno dosiahnuť pomocou jeden posun AC = c. Preto je logické písať a + b = c. Táto konštrukcia súčtu, c, a a b vedie k rovnakému výsledku ako zákon rovnobežníka, v ktorom je výsledná c daná diagonálnou AC rovnobežníka konštruovaného na vektoroch AB a AD ako strany. Pretože umiestnenie počiatočného bodu B vektora BC = b je nepodstatné, vyplýva z toho, že BC = AD. Obrázok 1 ukazuje, že AD + DC = AC, takže komutačný zákon
platí pre pridanie vektora. Takisto je ľahké dokázať, že asociatívne právo
je platný, a preto je možné zátvorky uvedené v bode (2) vynechať bez akýchkoľvek nejasností.
Ak s je skalár, sa alebo ako je definované ako vektor, ktorého dĺžka je | s || a | a ktorého smer je smer a, keď s je pozitívny a opačný ako smer a, ak s je negatívny. Takže a a-a sú vektory s rovnakou veľkosťou, ale opačným smerom. Predchádzajúce definície a dobre známe vlastnosti skalárnych čísel (predstavovaných s at) ukazujú, že

Pokiaľ sú zákony (1), (2) a (3) totožné so zákonmi, s ktorými sa stretávame v bežnej algebre, je celkom správne používať známe algebraické pravidlá na riešenie systémov lineárnych rovníc obsahujúcich vektory. Táto skutočnosť umožňuje odvodiť čisto algebraickými prostriedkami veľa teorémov syntetickej euklidovskej geometrie, ktoré si vyžadujú zložité geometrické konštrukcie.
Produkty vektorov.
Násobenie vektorov vedie k dvom typom produktov: bodový produkt a krížový produkt.
Bodkový alebo skalárny súčin dvoch vektorov aab, napísaný a · b, je skutočné číslo | a || b | cos (a, b), kde (a, b) označuje uhol medzi smermi a a b. geometricky,

Ak a a b sú v pravom uhle, potom a · b = 0, a ak ani a ani b nie je nulový vektor, potom zmiznutie bodového produktu ukazuje, že vektory sú kolmé. Ak a = b, potom cos (a, b) = 1 a a · a = | a | 2 udáva druhú mocninu dĺžky a.
Asociatívne, komutatívne a distribučné zákony elementárnej algebry platia pre bodové násobenie vektorov.
Kríž alebo vektorový produkt dvoch vektorov aab, napísaný a × b, je vektor
kde n je vektor dĺžky jednotky kolmý na rovinu aab a je nasmerovaný tak, aby pravotočivá skrutka otočená z a smerom k b postupovala v smere n (pozri obrázok 2). Ak a a b sú rovnobežné, a × b = 0. Veľkosť a × b môže byť reprezentovaná plochou rovnobežníka, ktorá má a a b ako susedné strany. Pretože rotácia z b na a je opačná ako rotácia z a do b,

To ukazuje, že krížový produkt nie je komutatívny, ale asociatívne právo (sa) × b = s (a × b) a distribučné právo
sú platné pre krížové produkty.
Súradnicové systémy.
Pretože empirické zákony fyziky nezávisia od špeciálnych alebo náhodných výberov referenčných rámcov vybraných tak, aby reprezentovali fyzikálne vzťahy a geometrické konfigurácie, vektorová analýza predstavuje ideálny nástroj na štúdium fyzikálneho vesmíru. Zavedenie špeciálneho referenčného rámca alebo súradnicového systému vytvára zhodu medzi vektormi a množinami čísiel predstavujúcich zložky vektorov v tomto rámci a vyvoláva určité pravidlá činnosti pre tieto súbory čísel, ktoré vyplývajú z pravidiel pre operácie na linke. segmenty.
Ak je vybraná určitá konkrétna sada troch nekolineárnych vektorov (nazývaných základné vektory), potom môže byť akýkoľvek vektor A jednoznačne vyjadrený ako uhlopriečka rovnobežníka, ktorého okraje sú zložkami A v smeroch základných vektorov. Bežne sa používa sada troch vzájomne kolmých jednotkových vektorov (tj vektorov s dĺžkou 1) i, j, k, smerovaných pozdĺž osí známeho karteziánskeho referenčného rámca (pozri obrázok 3). V tomto systéme má výraz tvar

kde x, y a z sú projekcie A na súradnicové osi. Keď sa dvaja vektory A 1 a A 2 sú reprezentované
potom použitie zákonov (3) vedie k ich súčtu

Tak, v kartézské ráme, súčet A 1 a A 2 je vektor určený (x 1 + y 1, x 2 + y 2, x 3 + y 3). Dá sa tiež napísať bodkový produkt
od tej doby
Použitie zákona (6) vedie k

takže krížový produkt je vektor určený trojnásobkom čísel, ktoré sa javia ako koeficienty i, j a k v (9).
Ak sú vektory reprezentované maticami 1 × 3 (alebo 3 × 1) pozostávajúcimi zo zložiek (x 1, x 2, x 3) vektorov, je možné preformulovať vzorce (7) až (9) v jazyku matice. Takéto preformulovanie naznačuje zovšeobecnenie pojmu vektor do priestorov dimenzionality vyšších ako tri. Napríklad stav plynu všeobecne závisí od tlaku p, objemu v, teploty T a času t. Štvornásobok čísel (p, v, T, t) nemôže byť reprezentovaný bodom v trojrozmernom referenčnom rámci. Ale pretože geometrická vizualizácia nehrá žiadnu úlohu v algebraických výpočtoch, obrazový jazyk geometrie sa môže stále použiť zavedením štvorrozmerného referenčného rámca určeného skupinou základných vektorov a 1, a 2, a 3, 4 so zložkami určenými pomocou riadky matice
Vo forme je potom reprezentovaný vektor x
takže v štvorrozmernom priestore je každý vektor určený štvornásobkom zložiek (x 1, x 2, x 3, x 4).








![Európska história bitky pri moste Stamford Bridge [1066] Európska história bitky pri moste Stamford Bridge [1066]](https://images.thetopknowledge.com/img/world-history/2/battle-stamford-bridge-european-history-1066.jpg)



